Triângulos Mapas Mentais – Matemática

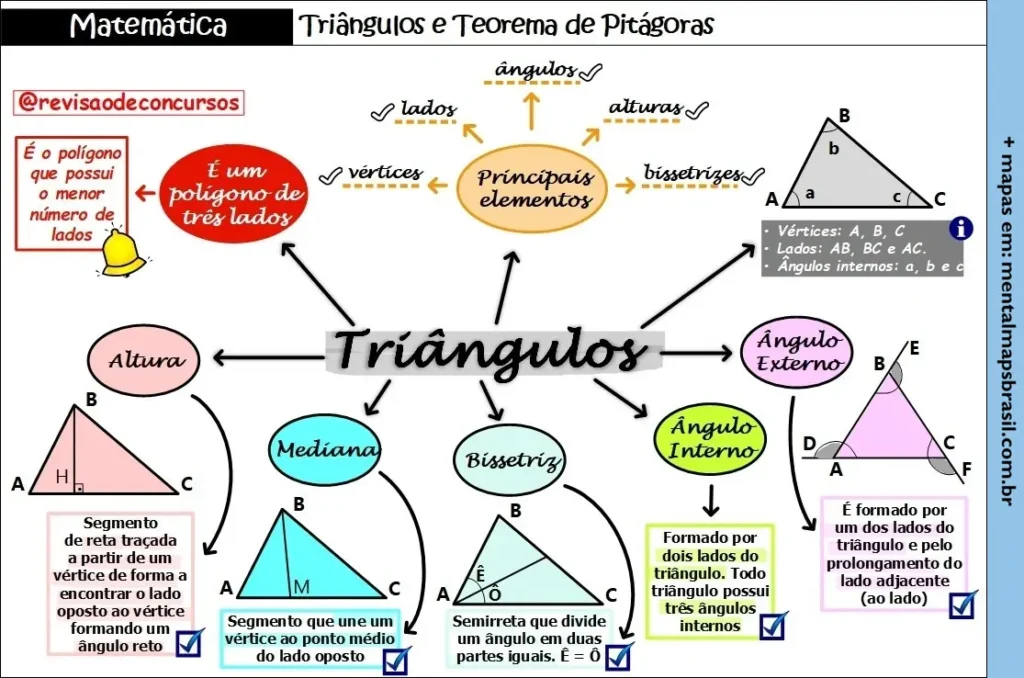
Transcrição do Mapa Mental sobre Triângulos e Teorema de Pitágoras

Principais elementos:

• Lados
• Vértices
• Ângulos
• Alturas
• Bissetrizes
  

Altura
Segmento de reta traçada a partir de um vértice de forma a encontrar o lado oposto ao vértice formando um ângulo reto.

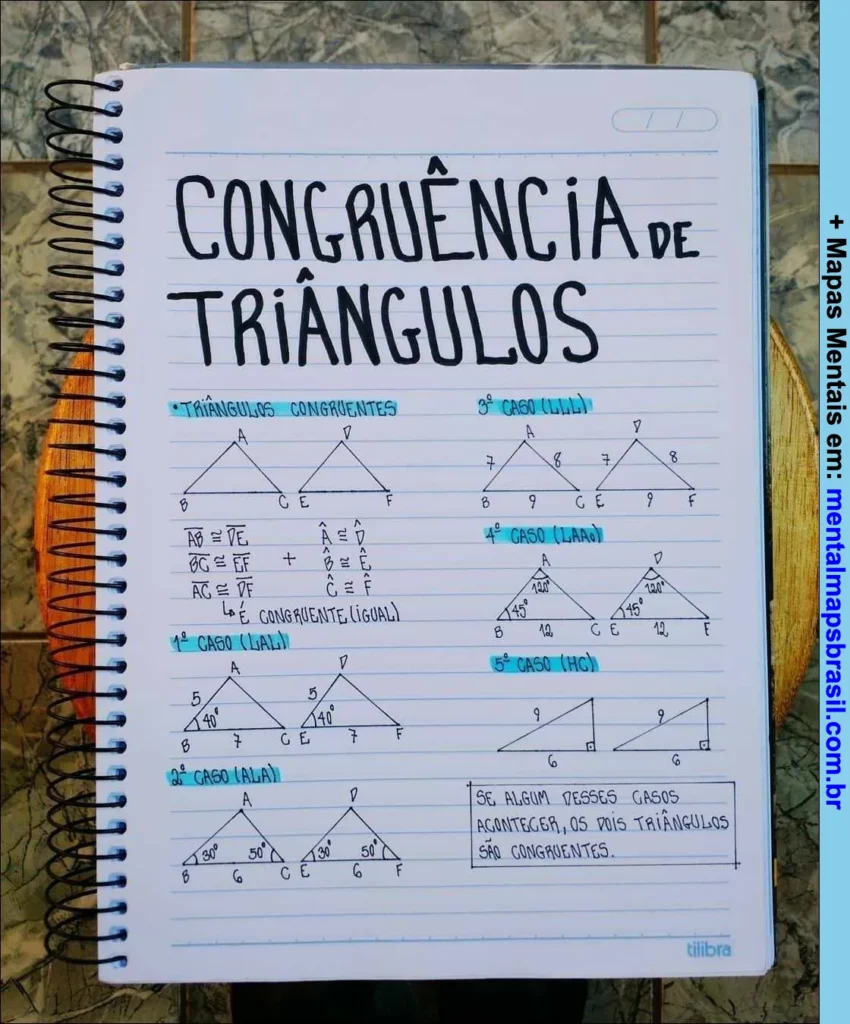
Transcrição do Mapa Mental sobre Congruência de Triângulos
Triângulos Congruentes
AB ≡ DE
BC ≡ EF
AC ≡ DF
É congruente (igual)
1º Caso (LAL)
2º Caso (ALA)
3º Caso (LAAng)
BC = EF
BC = EF ÂB = D̂
4º Caso (LLA)
5º Caso (HC)
Se algum desses casos acontecer, os dois triângulos são congruentes.

Transcrição do Mapa Mental sobre 5 EXPRESSÕES PARA A ÁREA DE UM TRIÂNGULO:

por base e altura
A = b.h/2
por dois lados e um ângulo
A = a.b.sen α/2
pelo semiperímetro
A = √p(p-a)(p-b)(p-c)
p = (a+b+c)/2
pelo raio r do círculo inscrito
A = p.r
pelo raio R do círculo circunscrito
A = a.b.c/4R

Transcrição do Mapa Mental sobre Relações Trigonométricas em um Triângulo Qualquer

As razões entre dois lados de um triângulo retângulo definem os números chamados seno, cosseno e tangente. Esses números estão associados a um dos ângulos agudos do triângulo, isto é, quando falamos do seno, do cosseno ou da tangente de um ângulo A, esse ângulo é um agudo em um triângulo retângulo.
Seno de um ângulo obtuso é o seno de seu suplemento ou senX= sen (180-x).
Cosseno de um ângulo obtuso é o posto do cosseno de seu suplemento ou cosX= -cos (180-x)
*O ângulo (resposta) sempre fica negativo.