Mapa Mental sobre Triângulo Retângulo: Trigonometria e Teorema de Pitágoras

Transcrição do Mapa Mental sobre TRIÂNGULO RETÂNGULO
RAZÕES TRIGONOMÉTRICAS
Cateto (b)
hipotenusa (h)
Cateto (a)
α + β = 90°
sen α = Ca/h
tg α = 1/tg β
a = h.sen β
b = h.cos β
Continue lendo…
Lembrar:
30° – sen: 1/2, cos: √3/2, tg: 1/√3
45° – sen: √2/2, cos: √2/2, tg: 1
60° – sen: √3/2, cos: 1/2, tg: √3
Macetes:
√2 se um ângulo for 45°
os catetos são iguais e a hipotenusa é cateto.√2
30° cateto oposto ao ângulo de 30° mede a metade da hipotenusa
RELAÇÕES MÉTRICAS
Teorema de Pitágoras
h² = m.n
a.h = b.c
c² = n.a
b² = m.a
a² = b² + c²
x² = d².l²
d = √l²
h = d.√2
h = l.√3/2
Mapa Mental sobre Relações Métricas: Trigonometria no Triângulo Retângulo

Transcrição do Mapa Mental sobre Relações Métricas no Triângulo Retângulo
m + n → Projeção
h → altura relativa a hipotenusa
a) b² = m.a → (Cat²) = (Proj).(hipot)
c² = n.a
b) h² = m.n → (Alt)² = (Proj).(Proj)
c) b.c = h.a → (Cat).(Cat) = (Alt).(Proj)
d) Teorema de Pitágoras → a² = b² + c²
Continue lendo…
Razões trigonométricas
Seno = Cateto Oposto/hipotenusa
Cosseno = Cateto Adjacente/hipotenusa
Tangente = Cateto Oposto/Cateto Adjacente
Ângulos Notáveis
30° | 45° | 60° | 90° | 180° | 270° | 360°
Sen: 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0
Cos: √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1
Tg: √3/3 | 1 | √3 | – | 0 | – | 0
Mapa Mental sobre Geometria Plana: Triângulos, Quadriláteros e Relações Métricas
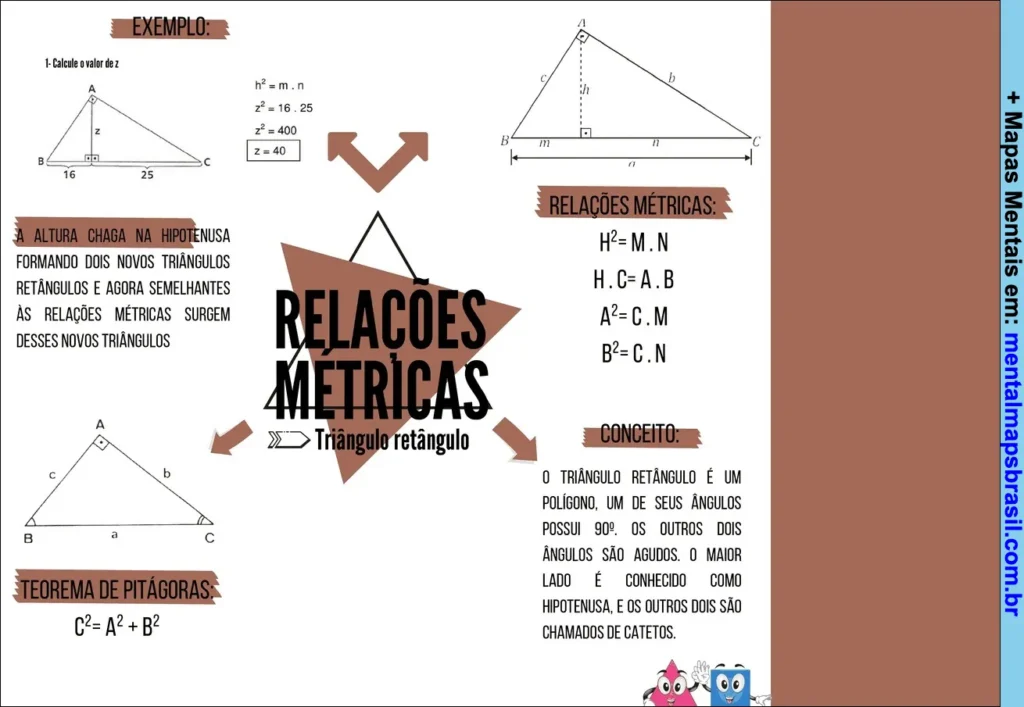
Transcrição do Mapa Mental sobre RELAÇÕES MÉTRICAS
Triângulo retângulo
EXEMPLO:
1- Calcule o valor de z
h² = m . n
z² = 16 . 25
z² = 400
z = 40
ALTURA CHEGA NA HIPOTENUSA FORMANDO DOIS NOVOS TRIÂNGULOS RETÂNGULOS E AGORA SEMELHANTES AS RELAÇÕES MÉTRICAS SURGEM DESSES NOVOS TRIÂNGULOS
Continue lendo…
RELAÇÕES MÉTRICAS:
H² = M . N
H . C = A . B
A² = C . M
B² = C . N
TEOREMA DE PITÁGORAS:
C² = A² + B²
CONCEITO:
O TRIÂNGULO RETÂNGULO É UM POLÍGONO, UM DE SEUS ÂNGULOS POSSUI 90º. OS OUTROS DOIS ÂNGULOS SÃO AGUDOS. O MAIOR LADO É CONHECIDO COMO HIPOTENUSA, E OS OUTROS DOIS SÃO CHAMADOS DE CATETOS.