Mapa Mental sobre Teoria dos Conjuntos
Transcrição do Mapa Mental sobre Teoria dos Conjuntos
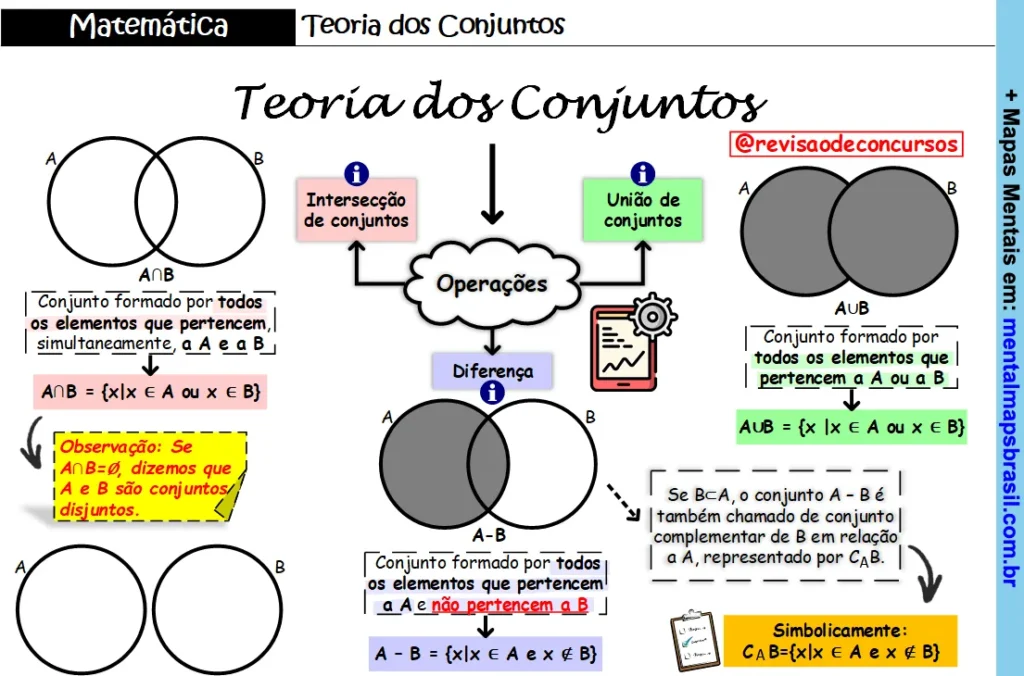
Operações:
Intersecção de conjuntos
União de conjuntos
Diferença
Intersecção de conjuntos:
Conjunto formado por todos os elementos que pertencem, simultaneamente, a A e a B
A∩B = {x|x ∈ A ou x ∈ B}
Continue lendo…
Observação: Se A∩B=∅, dizemos que A e B são conjuntos disjuntos.
União de conjuntos:
Conjunto formado por todos os elementos que pertencem a A ou a B
AUB = {x |x ∈ A ou x ∈ B}
Diferença:
Conjunto formado por todos os elementos que pertencem a A e não pertencem a B
A – B = {x|x ∈ A e x ∉ B}
Se B⊂A, o conjunto A – B é também chamado de conjunto complementar de B em relação a A, representado por CAB.
Simbolicamente:
CAB={x|x ∈ A e x ∉ B}
Mapa Mental sobre Conjuntos Matemática
Transcrição do Mapa Mental sobre Conjuntos
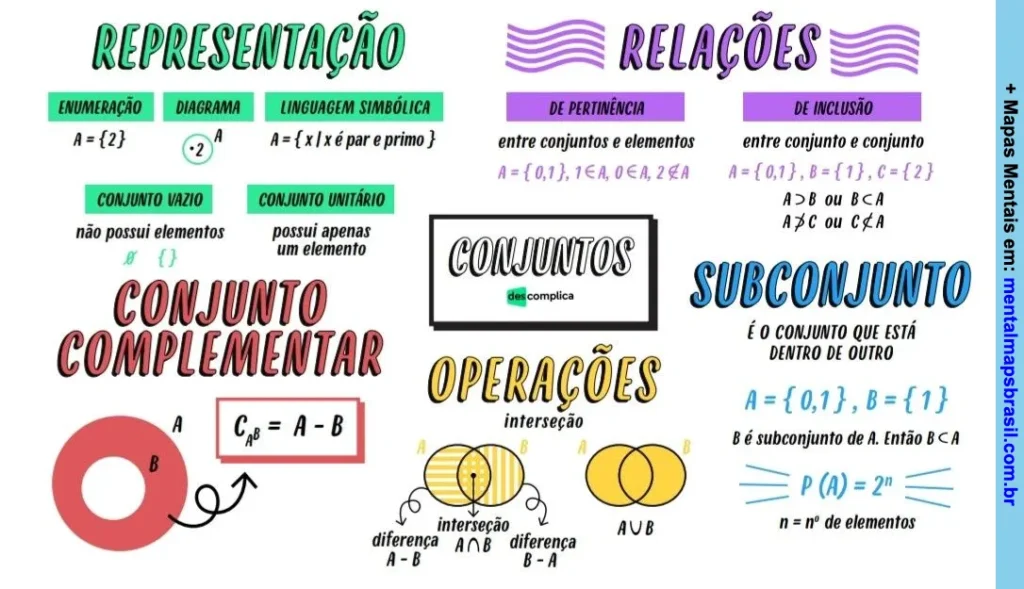
REPRESENTAÇÃO
ENUMERAÇÃO: A = {2}
DIAGRAMA: [Círculo com 2 dentro]
LINGUAGEM SIMBÓLICA: A = {x | x é par e primo}
CONJUNTO VAZIO: não possui elementos ∅ {}
CONJUNTO UNITÁRIO: possui apenas um elemento
Continue lendo…
RELAÇÕES
DE PERTINÊNCIA: entre conjuntos e elementos
A = {0,1}, 1∈A, 0∈A, 2∉A
DE INCLUSÃO: entre conjunto e conjunto
A = {0,1}, B = {1}, C = {2}
A⊃B ou B⊂A
A⊄C ou C⊄A
CONJUNTOS
desComplica
CONJUNTO COMPLEMENTAR
CAB = A – B [Diagrama mostrando A – B]
OPERAÇÕES
intersecção
[Diagrama de Venn mostrando intersecção A∩B, diferença A-B, e diferença B-A]
AUB [Diagrama de Venn mostrando união]
SUBCONJUNTO
É O CONJUNTO QUE ESTÁ DENTRO DE OUTRO
A = {0,1}, B = {1}
B é subconjunto de A. Então B⊂A
P(A) = 2n
n = nº de elementos
Mapa Mental sobre Conjuntos e Suas Representações Matemáticas

Transcrição do Mapa Mental sobre Conjuntos
O que são?
São as estruturas discretas fundamentais sobre as quais todas as demais estruturas discretas podem ser construídas. É a coleção não ordenada de objetos bem definidos (elementos, membros).
Teoria dos conjuntos
É capaz de representar toda a matemática.
Pertence / Não pertence
- a∈Aa \in Aa∈A: aaa pertence a AAA
- a∉Aa \notin Aa∈/A: aaa não pertence a AAA
Continue lendo…
Letras maiúsculas: conjuntos
Letras minúsculas: elementos
Formas de representar um conjunto
- {a,b,c}\{a, b, c\}{a,b,c}: entre chaves
- {x∈R∣x>2}\{x \in R | x > 2\}{x∈R∣x>2}: especificar uma propriedade que define o conjunto
- 1∈A1 \in A1∈A: definição recursiva
- x∈A↔x<3x \in A \leftrightarrow x < 3x∈A↔x<3
- M(A)={1,x>3}M(A) = \{1, x > 3\}M(A)={1,x>3}: especificar uma função característica
Obs: Nem sempre é possível utilizar todas as definições para um mesmo caso.
Alguns conjuntos importantes:
R,R+R, R^+R,R+ (não inclui o 0), Z,Q,N,CZ, Q, N, CZ,Q,N,C (números complexos).
Igualdade de conjuntos
Somente se tiverem os mesmos elementos. Não importando a ordem em que aparecem e se o mesmo elemento se repete.
A=B↔∀x:(x∈A↔x∈B)A = B \leftrightarrow \forall x: (x \in A \leftrightarrow x \in B)A=B↔∀x:(x∈A↔x∈B)
Subconjuntos
AAA é subconjunto de BBB somente se todos os elementos de AAA pertencem a BBB.
∀x:(x∈A↔x∈B)\forall x: (x \in A \leftrightarrow x \in B)∀x:(x∈A↔x∈B)
- “AAA é subconjunto de BBB”
- “BBB contém AAA”
- “AAA está contido em BBB”
Subconjuntos próprios
Todos os elementos de AAA pertencem a BBB, e existe pelo menos 1 elemento de BBB que não pertence a AAA.
∀x:(x∈A→x∈B)∧∃x:(x∈B∧x∉A)\forall x: (x \in A \rightarrow x \in B) \land \exists x: (x \in B \land x \notin A)∀x:(x∈A→x∈B)∧∃x:(x∈B∧x∈/A).
Diagramas de Venn
- A⊆BA \subseteq BA⊆B
- A⊈BA \not\subseteq BA⊆B
Mapa Mental sobre Conjuntos com definições e diagrama de Venn
Transcrição do Mapa Mental sobre Conjuntos
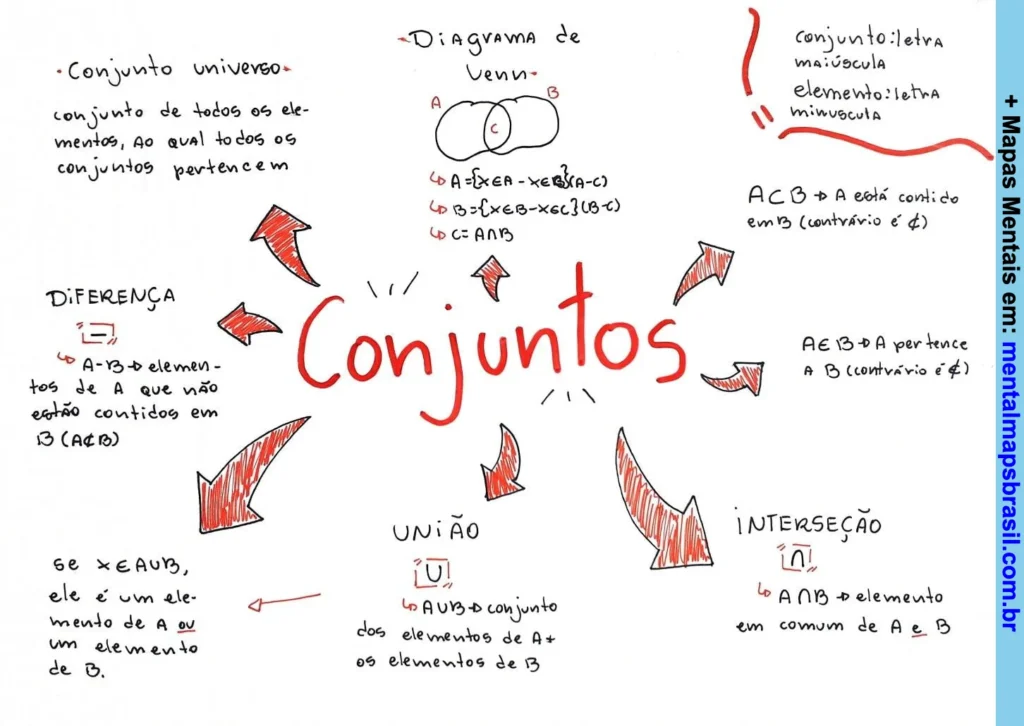
Conjunto universo:
- Conjunto de todos os elementos, ao qual todos os conjuntos pertencem.
Diferença:
- A – B → elementos de A que não estão contidos em B (A ∉ B).
- Se x ∈ A ∪ B, ele é um elemento de A ou um elemento de B.
União:
- A ∪ B → conjunto dos elementos de A + os elementos de B.
Continue lendo…
Interseção:
- A ∩ B → elemento em comum de A e B.
Diagrama de Venn:
- A = {x ∈ A – x ∉ B – x ∈ C}
- B = {x ∉ B – x ∈ C – x ∉ A}
- C = A ∩ B
Conjunto:
- Letra maiúscula.
Elemento: - Letra minúscula.
ACB:
- A está contido em B (contrário é ⊄).
A ∈ B:
- A pertence a B (contrário é ∉).
Mapa Mental sobre Conjuntos Numéricos e Exemplos de Aplicação
Transcrição do Mapa Mental sobre Conjuntos
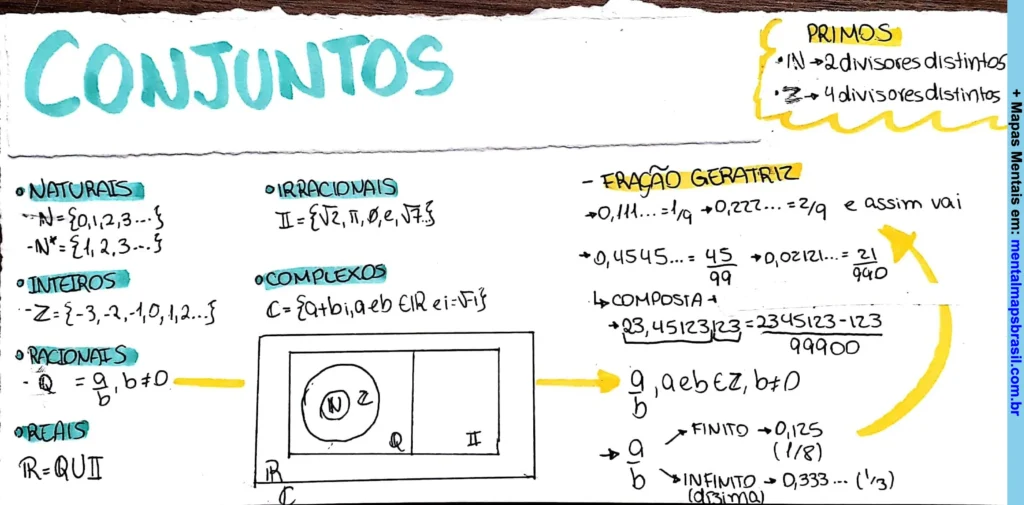
Naturais
- N = {0, 1, 2, 3…}
- N* = {1, 2, 3…}
Inteiros
- Z = {-3, -2, -1, 0, 1, 2…}
Racionais
- Q = a ÷ b, b ≠ 0
Continue lendo…
Reais
- R = Q ∪ II
Irracionais
- II = {√2, π, e, √7…}
Complexos
- C = a + bi, a e b ∈ R, i² = -1
Primos
- N → 2 divisores distintos.
- 3 → 4 divisores distintos.
Frações geratriz
- 0,222… = 2 ÷ 9
- 45 ÷ 99 = 0,4545…
- 21 ÷ 990 = 0,02121…
Composta
- 23,45 → 2345 – 23 ÷ 999
b ∈ Z, b ≠ 0
- Finito: 0,125 (1 ÷ 8).
- Infinito: 0,333… (1 ÷ 3).