Mapa Mental sobre Números Complexos: Conceitos e Aplicações
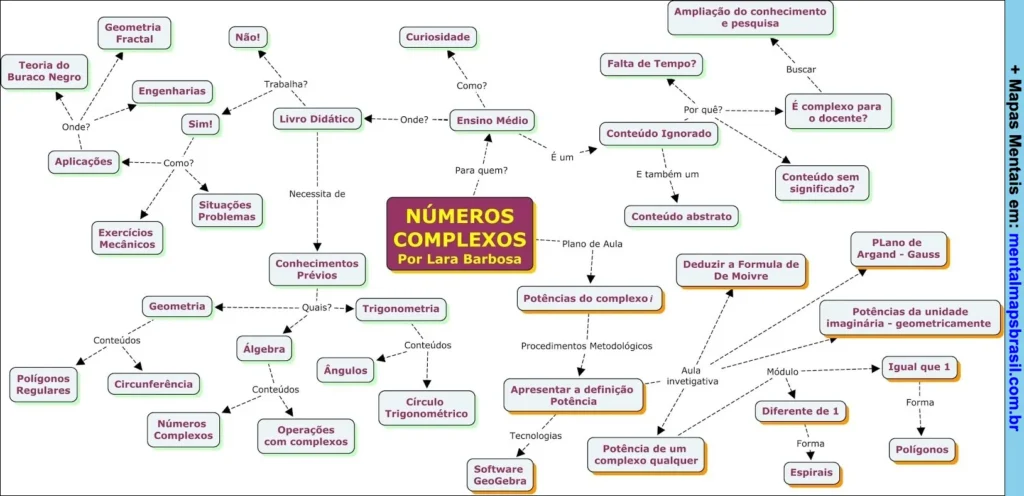
Transcrição do Mapa Mental sobre Números Complexos
Ensino Médio
Como?
Curiosidade
É complexo para o docente?
Ampliação do conhecimento e pesquisa
Conteúdo sem significado?
Conteúdo Ignorado
Falta de Tempo?
Conteúdo abstrato
Continue lendo…
Conhecimentos Prévios
Geometria
Polígonos Regulares
Circunferência
Trigonometria
Álgebra
Números Complexos
Operações com complexos
Ângulos
Círculo Trigonométrico
Livro Didático
Trabalha?
Sim!
Não!
Aplicações
Exercícios Mecânicos
Situações Problemas
Engenharias
Teoria do Buraco Negro
Geometria Fractal
Plano de Aula
Potências do complexo i
Apresentar a definição Potência
Software GeoGebra
Deduzir a Formula de De Moivre
Plano de Argand – Gauss
Potências da unidade imaginária – geometricamente
Igual que 1
Diferente de 1
Polígonos
Espirais
Mapa Mental sobre Números Complexos: Formas Algébrica e Trigonométrica

Transcrição do Mapa Mental sobre Números Complexos
Não tema os números complexos – eles são simples!
z = a + bi Forma Algébrica
a: parte real
bi: parte imaginária
Unidade imaginária!
i² = -1
Continue lendo…
Potências de i:
i⁰ = 1
i¹ = i
i² = -1
i³ = -i
Expoente maior que 3?
Divida por 4 e eleve ao resto!
Número real?
b = 0
Número imaginário puro?
a = 0 e b ≠ 0
- Conjugado
z̄ = a – bi - Norma
N = z.z̄ = a² + b² - Módulo
|z| = √N = √(a² + b²)
Plano de Argand-Gauss
Forma Trigonométrica
z = |z| · (cos θ + i·sen θ)
Mapa Mental sobre Números Complexos: Forma Trigonométrica
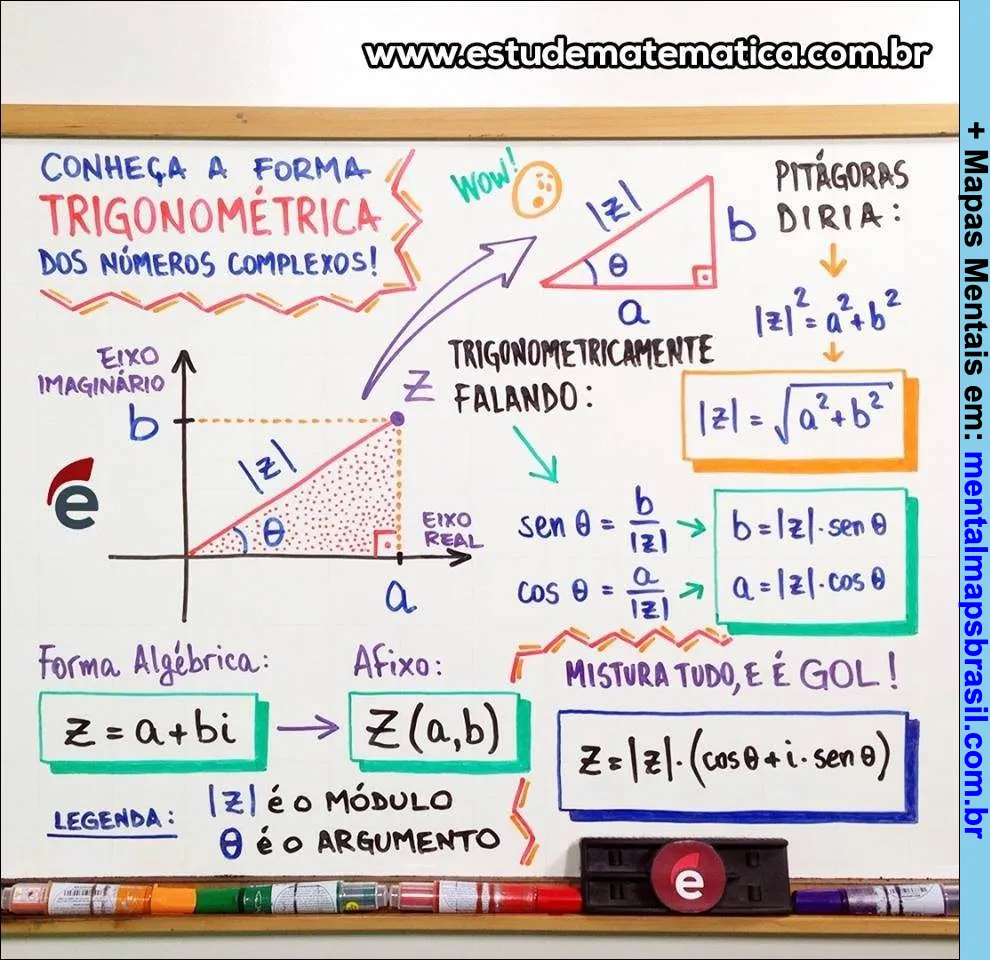
Transcrição do Mapa Mental sobre Conheça a forma trigonométrica dos números complexos!
Pitágoras diria:
|z|² = a² + b²
|z| = √(a² + b²)
Trigonometricamente falando:
sen θ = b/|z| → b = |z|·sen θ
cos θ = a/|z| → a = |z|·cos θ
Forma Algébrica:
z = a + bi
Continue lendo…
Afixo:
z(a,b)
Legenda:
|z| é o módulo
θ é o argumento
Mistura tudo, e é gol!
z = |z|·(cos θ + i·sen θ)