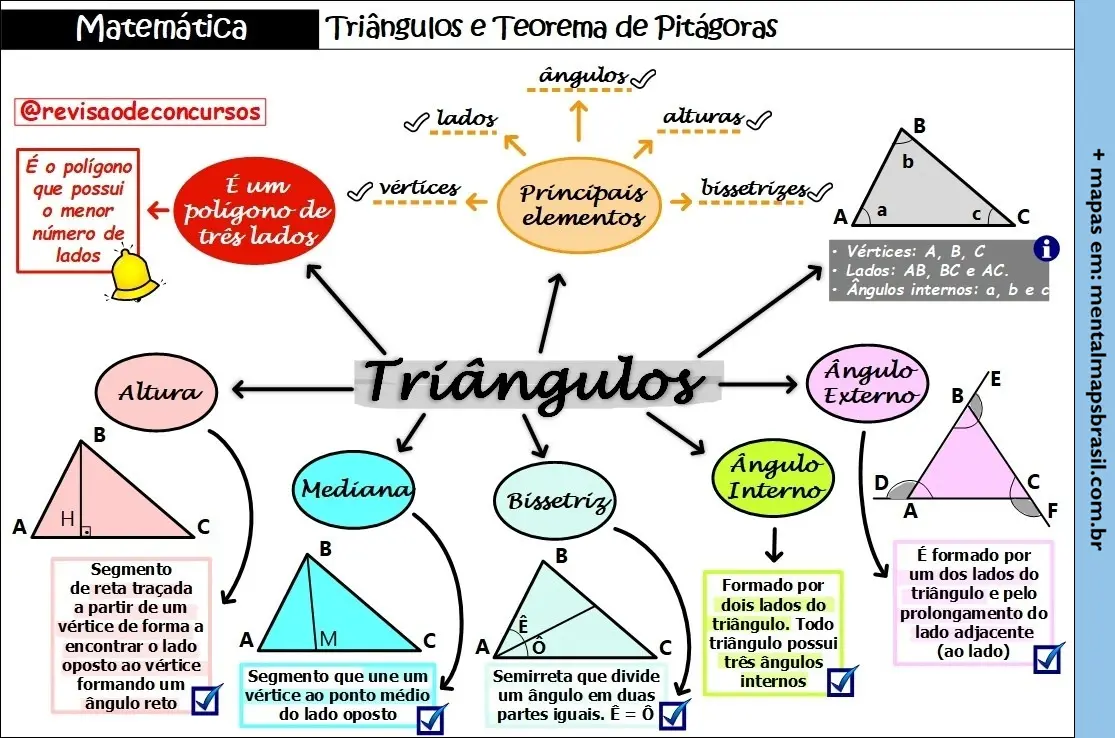
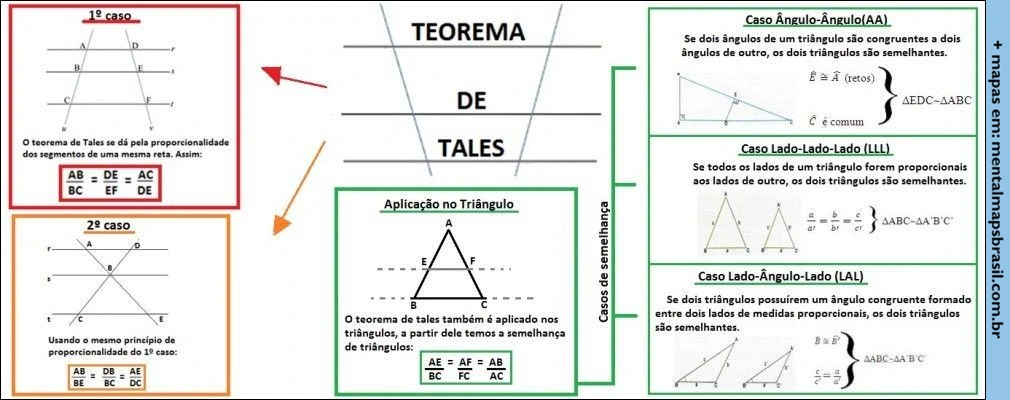
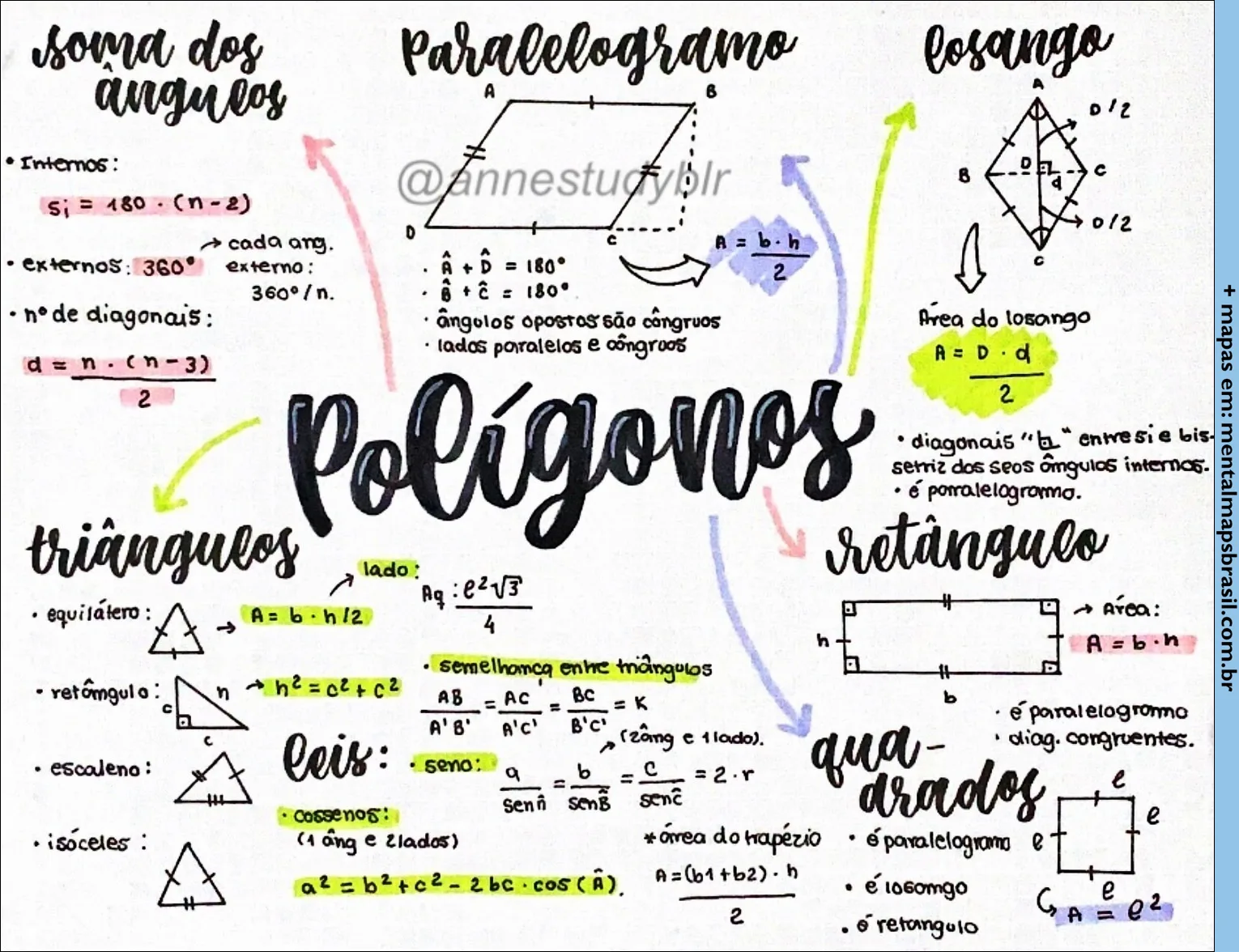
Regras de Sinais Mapas Mentais – Matemática
Cartaz explicando as Regras de Sinais em Matemática Transcrição do Mapa Mental sobre REGRA DE SINAIS Adição e Subtração Regra 1: Quando tiver um número positivo e o outro negativo, subtraia e coloque, no resultado final, o sinal do número que tiver maior valor. 40 – 60 = -20 (60 é maior que 40, então o … Leia mais…