Mapa Mental sobre Teorema de Tales
Transcrição do Mapa Mental sobre Teorema de Tales
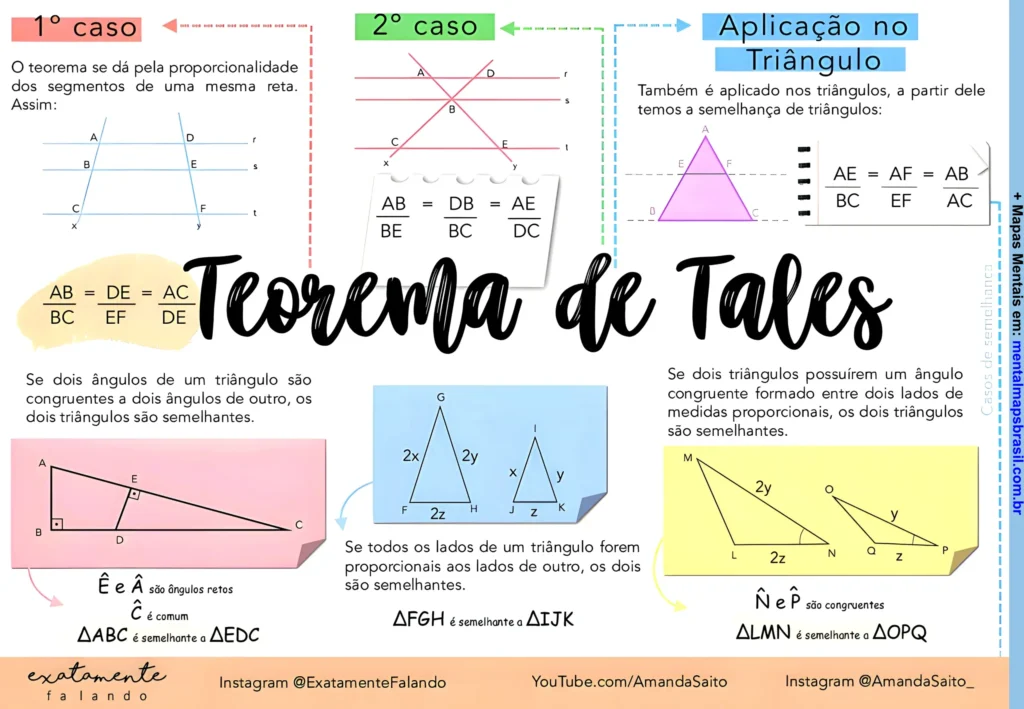
1º Caso
O teorema se dá pela proporcionalidade dos segmentos de uma mesma reta:
AB=DEAB=DE
BC=EFBC=EF
AC=DEAC=DE
Continue lendo…
2º Caso
Quando duas retas se cruzam:
- AB=DBAB=DB
- AE=DCAE=DC
- BCBC
Aplicação no Triângulo
Aplicado aos triângulos, temos a semelhança de triângulos:
- AE=AFAE=AF
- BC=EFBC=EF
- AB=ACAB=AC
Se dois triângulos possuem um ângulo congruente formado entre dois lados de medidas proporcionais, os triângulos são semelhantes.
Exemplo
- ΔFGHΔFGH é semelhante a ΔIJKΔIJK
Se todos os lados de um triângulo forem proporcionais aos lados de outro, os dois são semelhantes.
Outro Exemplo
- ΔLMNΔLMN é semelhante a ΔOPQΔOPQ
Nota
Se E^E^ e P^P^ são congruentes, então ΔLMNΔLMN é semelhante a ΔOPQΔOPQ.
Diagrama sobre o Teorema de Tales
Transcrição do Diagrama sobre Teorema de Tales:
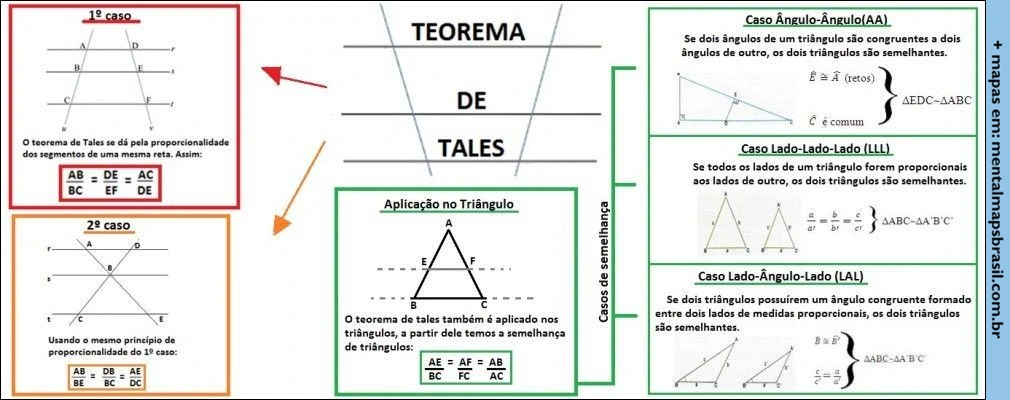
1º caso
O teorema de Tales se dá pela proporcionalidade dos segmentos de uma mesma reta. Assim:
AB/BC = DE/EF
2º caso
Usando o mesmo princípio de proporcionalidade de 1º caso:
AB/BE = DC/DE
Continue lendo…
Aplicação no Triângulo
O teorema de Tales também é aplicado nos triângulos, a partir dele temos os casos de semelhança de triângulos:
Caso Ângulo-Ângulo (AA)
Se dois ângulos de um triângulo são congruentes a dois ângulos de outro, os dois triângulos são semelhantes.
Caso Lado-Lado-Lado (LLL)
Se todos os lados de um triângulo forem proporcionais a todos os lados de outro, os dois triângulos são semelhantes.
Caso Lado-Ângulo-Lado (LAL)
Se dois triângulos possuírem um ângulo congruente formado entre dois lados de medidas proporcionais, os dois triângulos são semelhantes.