Mapa Mental sobre Geometria Plana
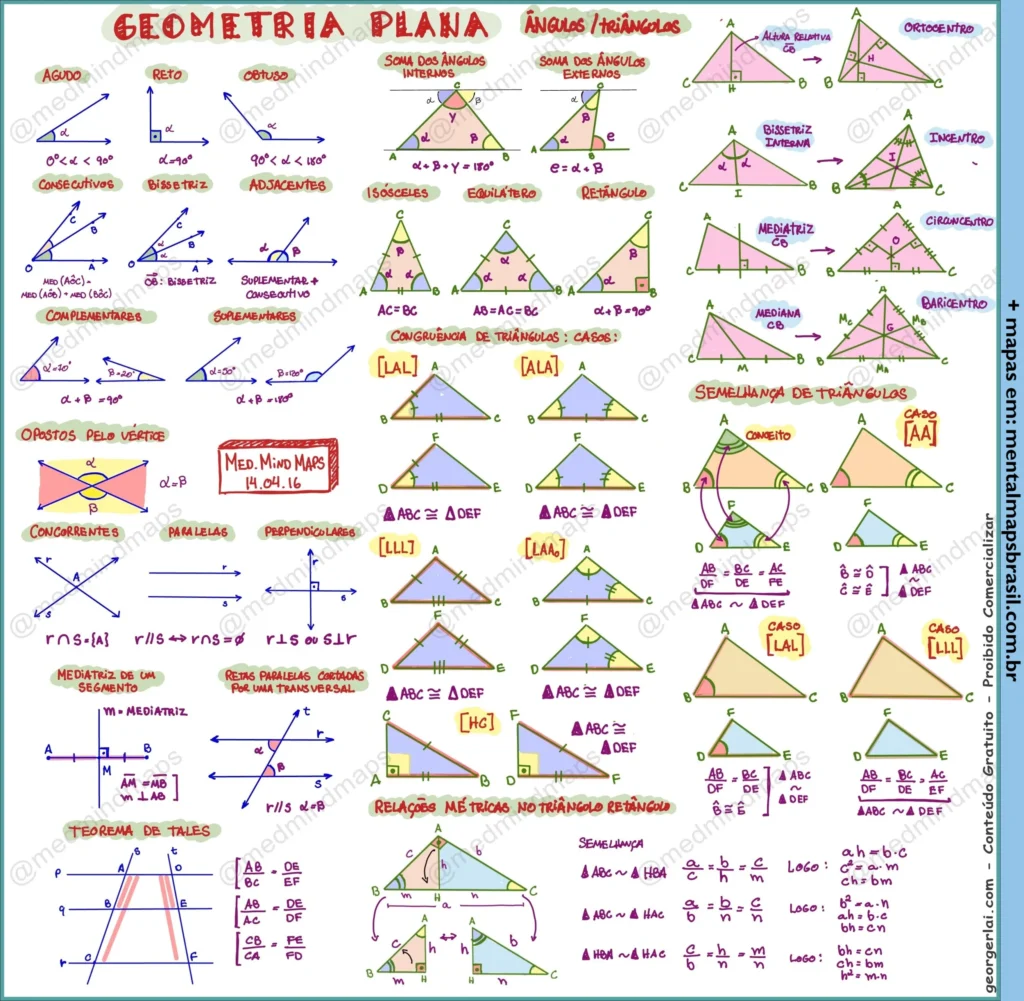
Mapa mental sobre Geometria Plana apresenta conceitos fundamentais, incluindo ângulos (agudos, obtusos e retos) e triângulos (isósceles, equilátero e retângulo). O conteúdo abrange a soma dos ângulos internos e externos, além de casos de congruência (LAL, ALA, LLL) e semelhança de triângulos. O Teorema de Tales e suas aplicações são destacados, juntamente com relações métricas em triângulos.
Mapa Mental sobre Geometria Plana com Trapézios, Polígonos e Circunferências
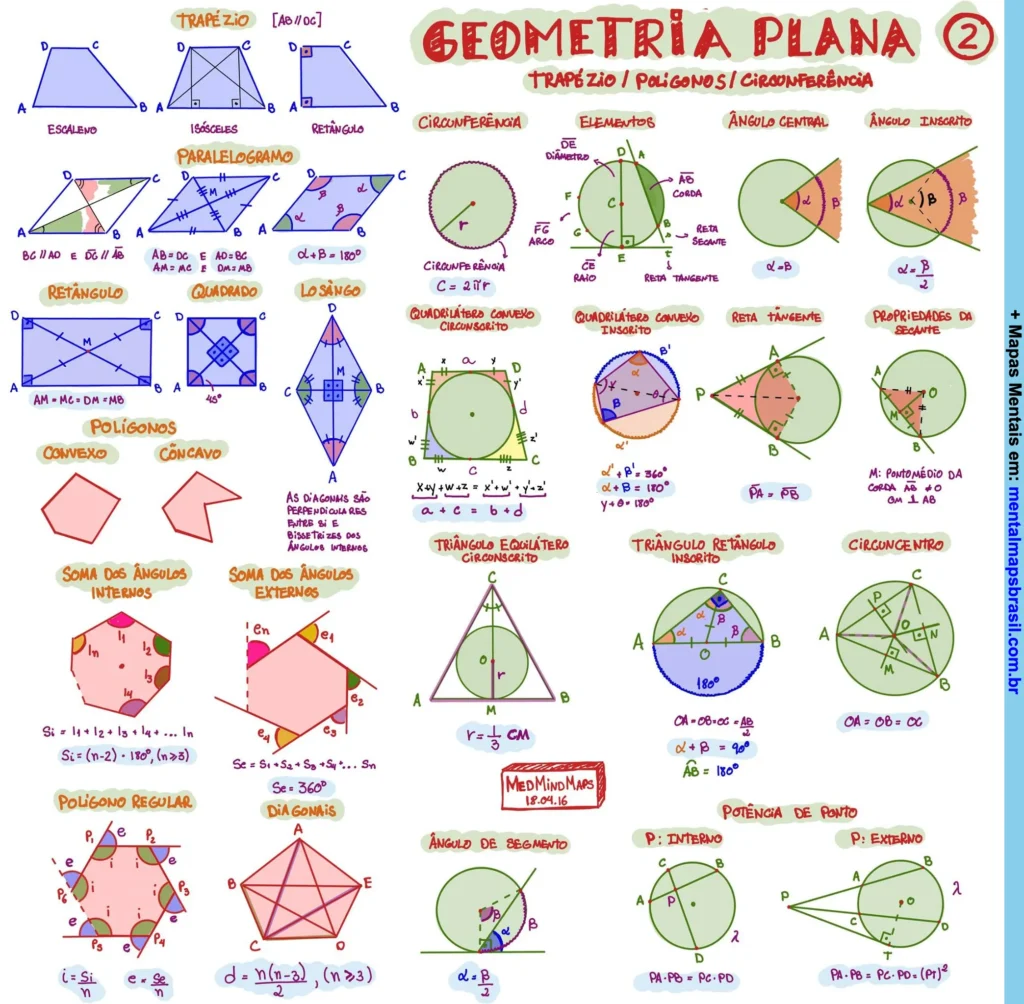
Transcrição do Mapa Mental sobre Geometria Plana
Trapézio / Polígonos / Circunferência
- Trapézio
- Escaleno
- Isósceles
- Retângulo
- Paralelogramo
- BC = AD; BD = AC
- Ângulos opostos são iguais
- AB // CD; BC // AD
Continue lendo…
Retângulo, Quadrado, Losango
- AM = MC = DM = MB
- Ângulo reto, lados iguais
Polígonos Convexo e Côncavo
Soma dos Ângulos Internos
Si = (n-2) · 180°
Soma dos Ângulos Externos
Se = 360°
Polígono Regular
Ângulo Interno = Si / n
Ângulo Externo = Se / n
Diagonal
d = n(n-3)/2
Circunferência
- Elementos: raio, diâmetro, arco, corda.
- Ângulo Central e Ângulo Inscrito
- Quadrilátero Convexo Circunscrito
- Quadrilátero Convexo Inscrito
- Reta Tangente
Triângulo Equilátero Circunscrito
r = l · √3 / 6
R = l · √3 / 3
Triângulo Retângulo Inscrito
Ângulo reto inscrito na semicircunferência.
Potência de Ponto
P: Externo → PA · PB = PC · PD
P: Interno → PA · PB = PC · PD
Mapa Mental sobre Geometria Plana e Cálculo de Áreas.
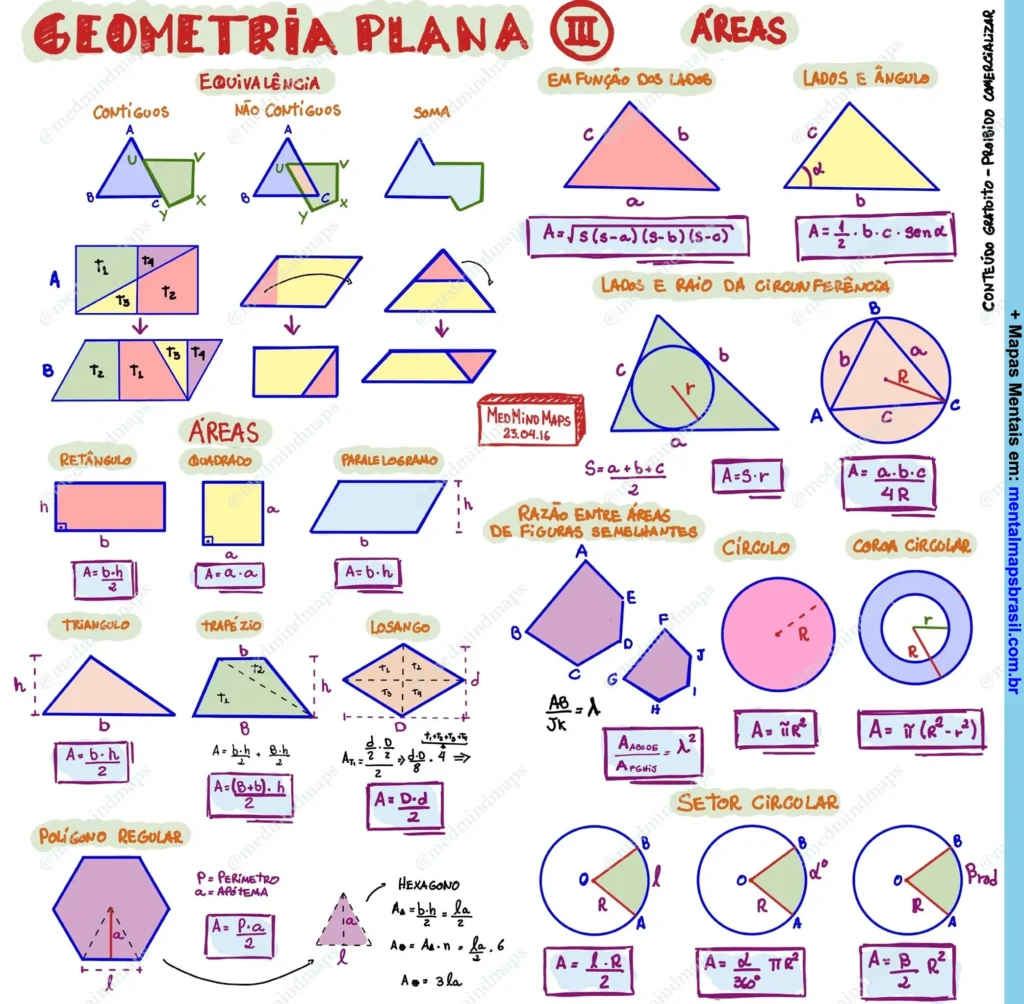
Transcrição do Mapa Mental sobre Geometria Plana III – Áreas
- Equivalência
- Contíguos.
- Não contíguos.
- Soma.
- Áreas em função dos lados
- Triângulo:
- A = √s(s – a)(s – b)(s – c).
- Lados e ângulo:
- A = ½ · b · c · senα.
- Triângulo:
Continue lendo…
Lados e raio da circunferência
Triângulo:
A = r · s.
A = a · b · c / 4R.
Áreas
- Retângulo: A = b · h.
- Quadrado: A = a².
- Paralelogramo: A = b · h.
- Triângulo: A = b · h / 2.
- Trapézio: A = (B + b) · h / 2.
- Losango: A = D · d / 2.
- Polígono regular:
- P = perímetro.
- A = P · a / 2.
- Hexágono:
- A = 3a²√3 / 2.
Razão entre áreas de figuras semelhantes
- A1 / A2 = (l1 / l2)².
Círculo
- A = πR².
Coroa circular
- A = π(R² – r²).
Setor circular
A = (AB / 2) · R.
A = (l / 360°) · πR².
Mapa Mental sobre Geometria Plana com desenhos
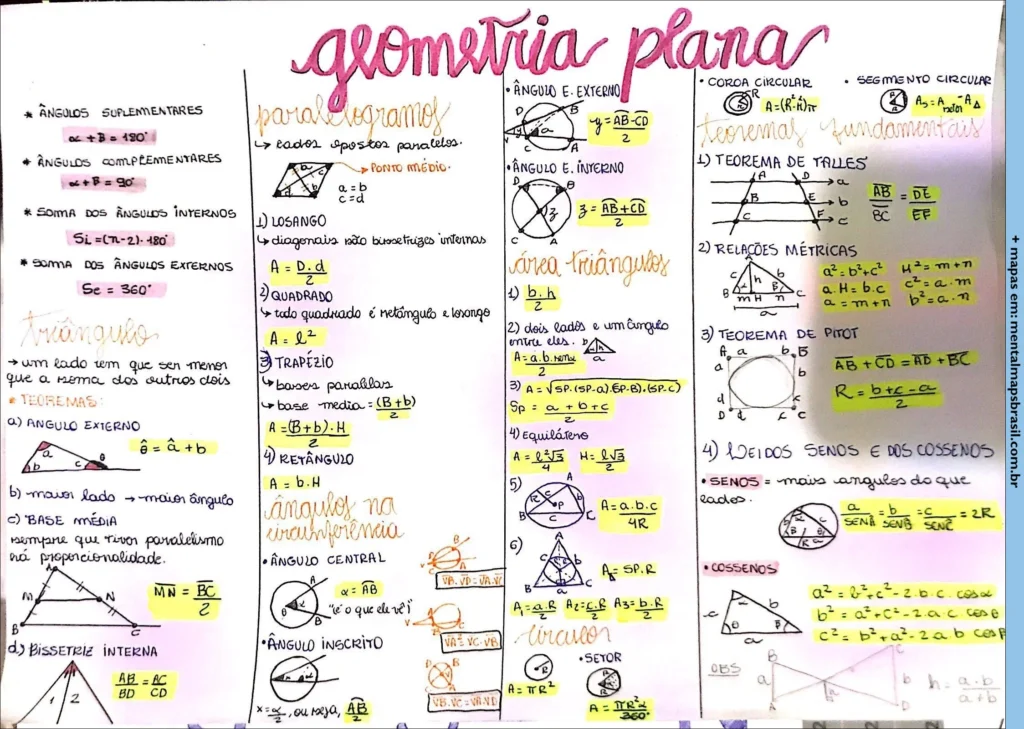
Mapa mental sobre Geometria Plana abordando conceitos essenciais como ângulos suplementares e complementares, além da soma dos ângulos internos e externos de um triângulo. Detalha as propriedades de paralelogramos, incluindo losangos, quadrados, trapézios e retângulos, com fórmulas para cálculo de áreas. O conteúdo inclui também o Teorema de Tales e relações métricas em triângulos, além das fórmulas para ângulos em circunferências.
Mapas Mentais sobre Geometria Plana: ângulos, triângulos, áreas, opostos e teorema de Tales
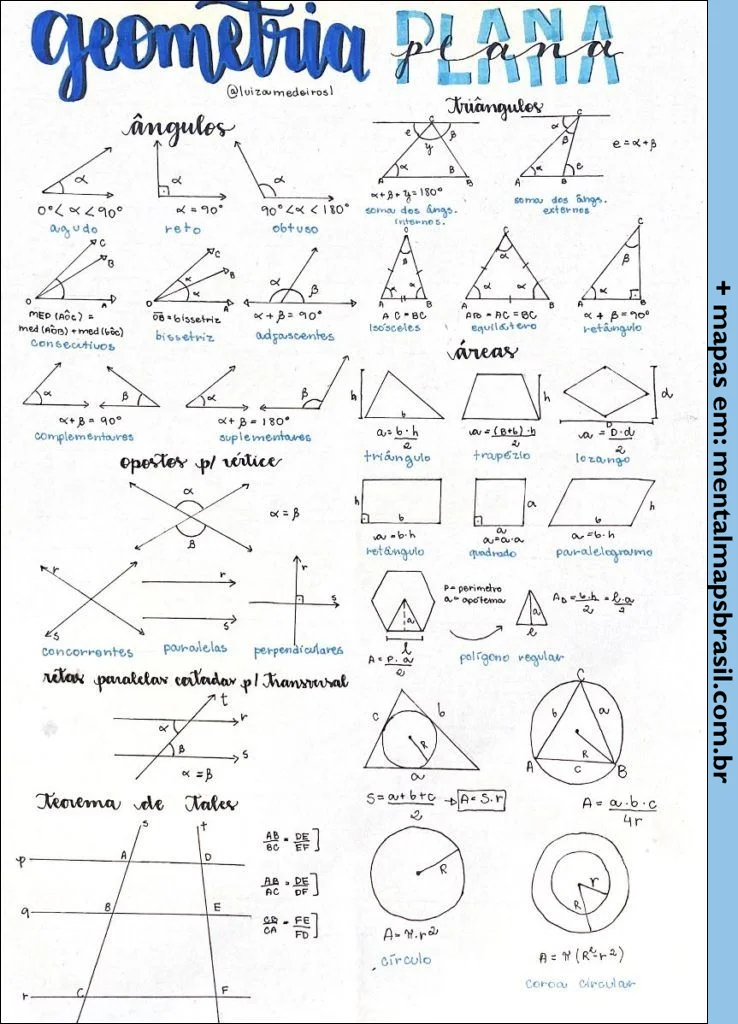
Mapa mental sobre Geometria Plana explorando conceitos essenciais, incluindo tipos de ângulos (agudos, retos e obtusos) e classificações de triângulos (isósceles, equilátero e retângulo). Apresenta fórmulas para cálculo de áreas de figuras geométricas como triângulos, trapézios, losangos, retângulos e quadrados. O conteúdo também aborda relações entre ângulos formados por retas paralelas cortadas por uma transversal. O Teorema de Tales é destacado, com aplicações práticas.
Mapa Mental sobre Triângulos e Quadriláteros
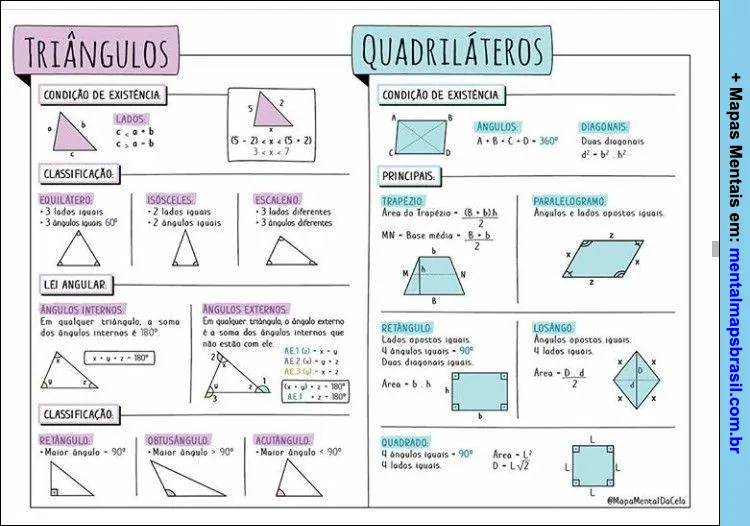
Transcrição do Mapa Mental sobre TRIÂNGULOS
CONDIÇÃO DE EXISTÊNCIA
LADOS: c < a + b
ÂNGULOS: α + β + γ = 180°
CLASSIFICAÇÃO
EQUILÁTERO: 3 lados iguais, 3 ângulos iguais 60°
ISÓSCELES: 2 lados iguais, 2 ângulos iguais
ESCALENO: 3 lados diferentes, 3 ângulos diferentes
Continue lendo…
LEI ANGULAR
ÂNGULOS INTERNOS: Em qualquer triângulo, a soma dos ângulos internos é 180°
ÂNGULOS EXTERNOS: Em qualquer triângulo, o ângulo externo é igual à soma dos dois ângulos internos que não estão com ele
AEI = α + γ = 180°
AE2 = β + γ = 180°
AE3 = α + β = 180°
CLASSIFICAÇÃO
RETÂNGULO: Maior ângulo = 90°
OBTUSÂNGULO: Maior ângulo > 90°
ACUTÂNGULO: Maior ângulo < 90°
QUADRILÁTEROS
CONDIÇÃO DE EXISTÊNCIA
ÂNGULOS: A + B + C + D = 360°
DIAGONAIS: Duas diagonais d = 2 x 2
PRINCIPAIS
TRAPÉZIO: Área do trapézio = (B + b).h/2
PARALELOGRAMO: Ângulos e lados opostos iguais
RETÂNGULO: Lados opostos iguais, 4 ângulos iguais = 90°, Duas diagonais iguais, Área = b x h
LOSANGO: Ângulos opostos iguais, 4 lados iguais, Área = D.d/2
QUADRADO: 4 ângulos iguais = 90°, 4 lados iguais, Área = L²
Mapa Mental sobre Geometria Plana e Classificação dos Triângulos
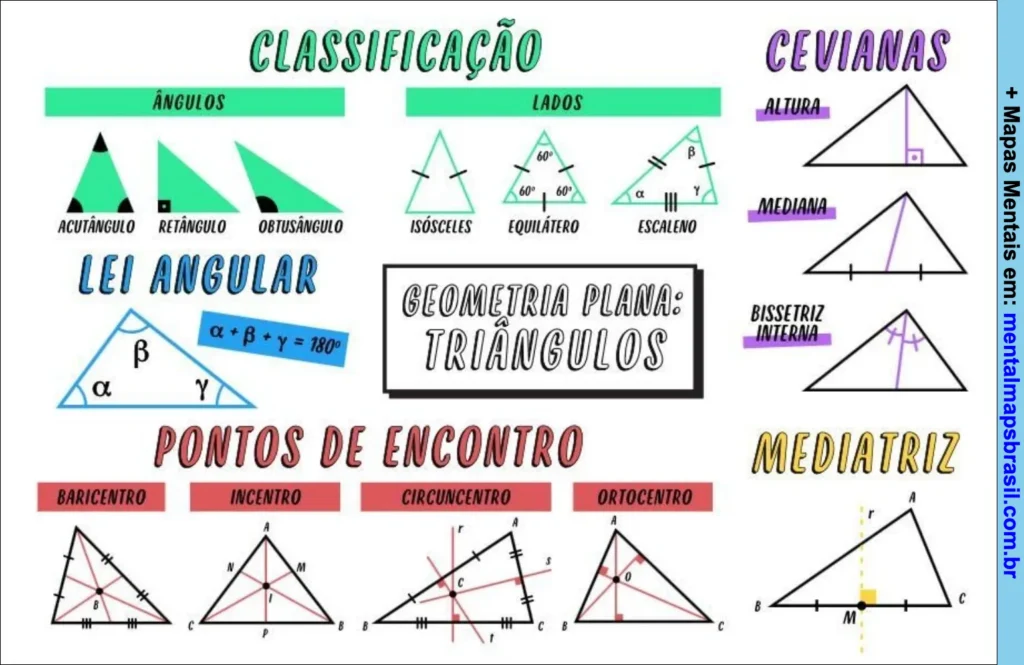
Transcrição do Mapa Mental sobre Geometria Plana
Classificação
Ângulos
- Acutângulo
- Retângulo
- Obtusângulo
Lados
- Isósceles
- Equilátero
- Escaleno
Continue lendo…
Lei Angular
α + β + γ = 180°
Geometria Plana: Triângulos
Cevianas
- Altura
- Mediana
- Bissetriz interna
Pontos de encontro
- Baricentro
- Incentro
- Circuncentro
- Ortocentro
Mediatriz