Mapa Mental sobre Congruência e Semelhança
Transcrição do conteúdo do mapa mental sobre Congruência e Semelhança:
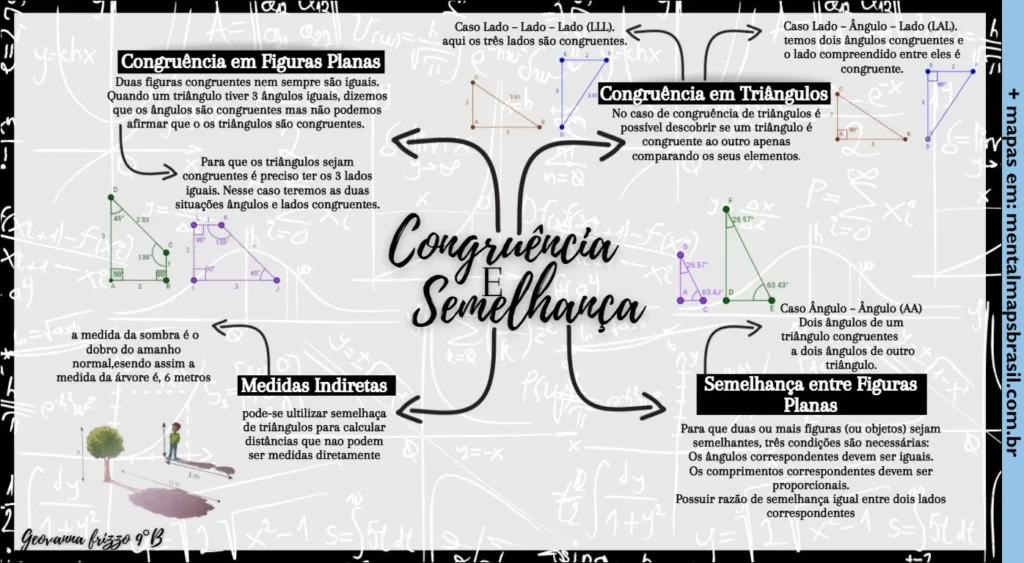
Congruência em Figuras Planas
Duas figuras congruentes nem sempre são iguais. Quando um triângulo tiver 3 ângulos iguais, dizemos que os ângulos são congruentes mas não podemos afirmar que o os triângulos são congruentes.
Continue lendo…
Para que os triângulos sejam congruentes é preciso ter os 3 lados iguais. Nesse caso teremos as duas situações ângulos e lados congruentes.
Congruência em Triângulos
No caso de congruência de triângulos é possível descobrir se um triângulo é congruente ao outro apenas comparando os seus elementos.
Caso Lado – Lado – Lado (LLL).
aqui os três lados são congruentes.
Caso Lado – Ângulo – Lado (LAL).
temos dois ângulos congruentes e o lado compreendido entre eles é congruente.
Caso Ângulo – Ângulo (AA)
Dois ângulos de um triângulo congruentes a dois ângulos de outro triângulo.
Medidas Indiretas
pode-se utilizar semelhança de triângulos para calcular distâncias que não podem ser medidas diretamente
a medida da sombra é o dobro do amanho normal,sendo assim a medida da árvore é, 6 metros
Semelhança entre Figuras Planas
Para que duas ou mais figuras (ou objetos) sejam semelhantes, três condições são necessárias:
Os ângulos correspondentes devem ser iguais.
Os comprimentos correspondentes devem ser proporcionais.
Possuir razão de semelhança igual entre dois lados correspondentes