Mapa Mental sobre Grandezas Físicas: Vetores
Transcrição do Mapa Mental sobre Grandezas Físicas: Vetores
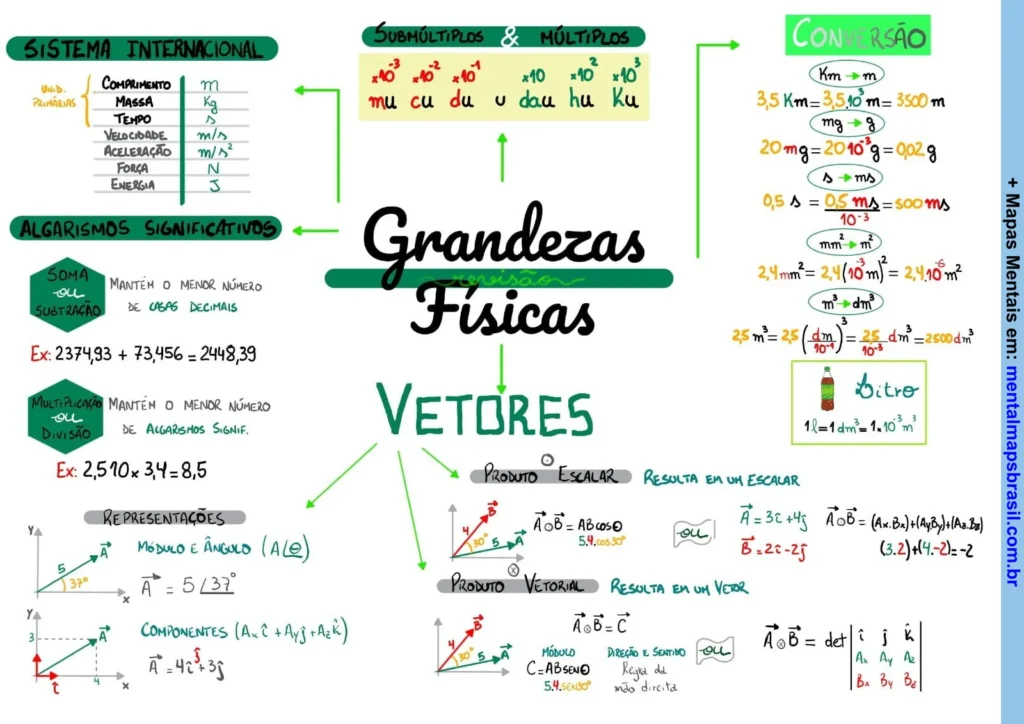
Sistema Internacional
Energia: J
Comprimento: m
Massa: kg
Tempo: s
Velocidade: m/s
Aceleração: m/s²
Força: N
Continue lendo…
Submúltiplos & Múltiplos
- μμ (micro): 10−610−6
- cc (centi): 10−210−2
- dd (deci): 10−110−1
- dada (decâmetro): 101101
- hh (hectô): 102102
- KK (quilo): 103103
Conversão
- 3,5 km=3,5×103 m3,5km=3,5×103m
- 20 mg=20×10−3 g20mg=20×10−3g
- 0,5 s=0,5 ms=500 µs0,5s=0,5ms=500µs
- 2,4 m2=2,4×100 m2=2,4×10−6 m22,4m2=2,4×100m2=2,4×10−6m2
- 25 cm3=25 dm3=2500 cm325cm3=25dm3=2500cm3
Vetores
Representações
- Módulo e Ângulo (A,θ)(A,θ)
- A⃗=5 mA=5m a 37∘37∘
Componentes
- A⃗=Ax+Ay+AzA=Ax+Ay+Az
Produto Escalar
- A⃗⋅B⃗=ABcosθA⋅B=ABcosθ
- Resulta em um escalar.
Produto Vetorial
Resulta em um vetor.
A⃗×B⃗=C⃗A×B=C
Mapa Mental sobre Vetores: Conceitos Fundamentais e Aplicações na Física e Matemática
Transcrição do Mapa Mental sobre Vetores
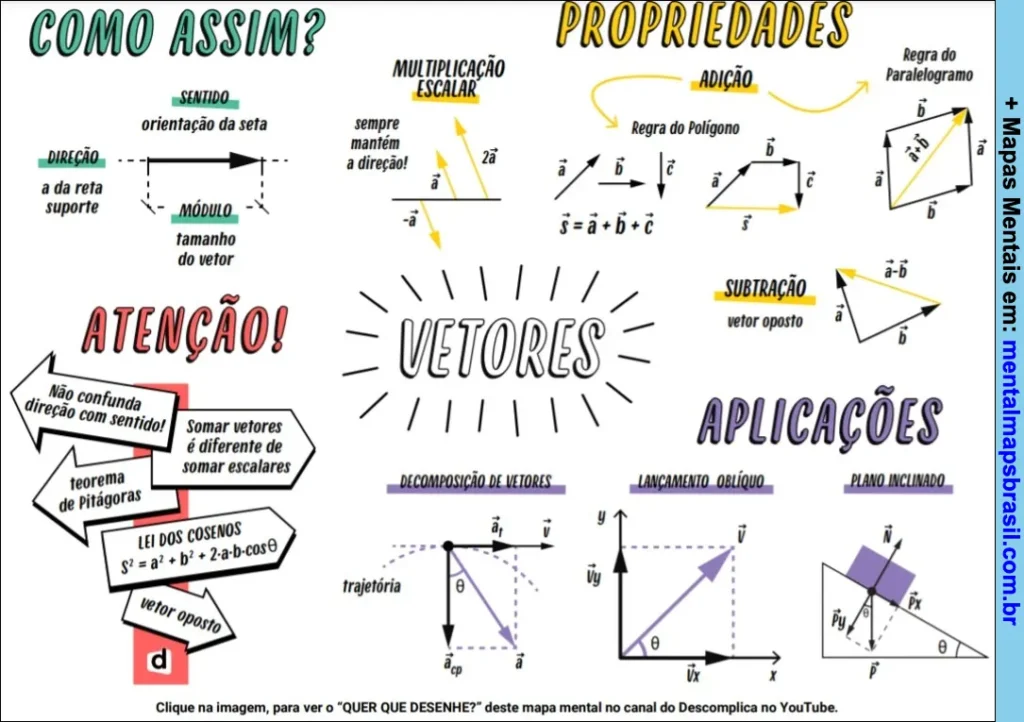
COMO ASSIM?
SENTIDO
orientação da seta
DIREÇÃO
a da reta suporte
MÓDULO
tamanho do vetor
Continue lendo…
PROPRIEDADES
MULTIPLICAÇÃO ESCALAR
sempre mantém a direção!
2a
-a
ADIÇÃO
Regra do Polígono
s = a + b + c
Regra do Paralelogramo
SUBTRAÇÃO
vetor oposto
a-b
VETORES
ATENÇÃO!
Não confunda direção com sentido!
Somar vetores é diferente de somar escalares
teorema de Pitágoras
LEI DOS COSENOS
S² = a² + b² + 2ab·cosθ
vetor oposto
APLICAÇÕES
DECOMPOSIÇÃO DE VETORES
trajetória
LANÇAMENTO OBLÍQUO
PLANO INCLINADO
Mapa Mental sobre Vetores: Conceitos Fundamentais e Lei dos Cossenos

Transcrição do Mapa Mental sobre VETORES
CONCEITO
Segmento de reta orientado por três características.
Módulo
Tamanho, valor.
Direção
Reta: horizontal ou vertical.
Sentido
Seta: direita, esquerda, pra cima, pra baixo.
Continue lendo…
Obs.: Vetor oposto, ou seja, com sinal negativo, inverte o sentido do segmento de reta.
ESCALAR
• Quando conhecemos a medida.
• Massa, energia, distância, área, volume.
VETORIAL
• Quando tem direção e sentido.
• deslocamento, velocidade, aceleração, força, quantidade de movimento.
Exemplo: a = 8cm
a → |a| = 8 cm
2a → |2a| = 16 cm
3a → |3a| = 24 cm
Vetor Oposto:
-a → |-a| = 8 cm
-2a → |-2a| = 16 cm
Lei dos Cossenos
[Diagrama de um triângulo com ângulos α, β, γ]
a² = b² + c² – 2bc · cos α
b² = a² + c² – 2ac · cos β
c² = a² + b² – 2ab · cos γ
Resumo sobre Vetores e Operações Matemáticas

Transcrição do Mapa Mental sobre Vetores
- Grandeza vetorial
- É conhecer o valor da sua medida, a unidade, a direção e o sentido.
- Vetores
- É um segmento de reta que apresenta uma orientação.
- Intensidade: Valor numérico.
- Direção: Reta onde o vetor está localizado.
- Sentido: Para onde o vetor atua de acordo com sua direção.
Continue lendo…
Vetores iguais
- Dois ou mais vetores são iguais quando possuem o mesmo módulo, a mesma direção e o mesmo sentido.
Vetores opostos
- Dois vetores são opostos quando possuem o mesmo módulo, a mesma direção, mas sentidos contrários.
Vetores ortogonais
- Dois vetores são ortogonais quando formam um ângulo de 90º entre si.
Operações
- Adição: Polígono.
- Resultado das forças aplicadas no corpo.
- Adição: Paralelogramo.
Mapa Mental sobre Vetores e Propriedades Matemáticas
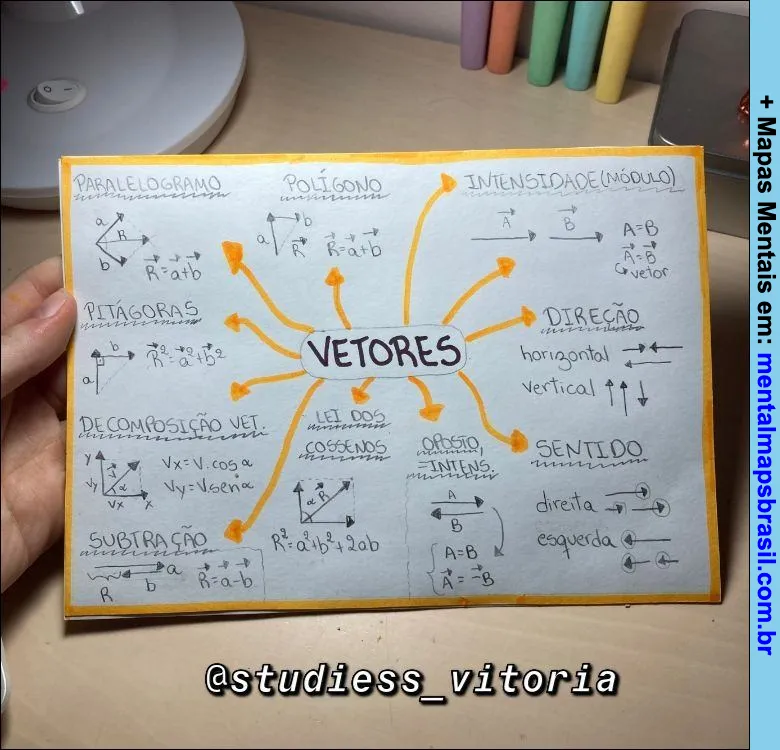
Transcrição do Mapa Mental sobre Vetores:
- Paralelogramo
- Polígono
- Intensidade (Módulo):
- |A|
- A = B
- R² = a² + b²
- Direção:
- Horizontal
- Vertical
Continue lendo…
Sentido:
- Direita
- Esquerda
Pitagoras:
- R² = a² + b²
Decomposição Vet.:
- Vx = V . cos α
- Vy = V . sen α
Subtração:
- R² = a² + b²
- R = a – b
Lei dos CossenosOposto Intens.