Mapa Mental sobre a Lei dos Senos e dos Cossenos
Transcrição do Mapa Mental sobre Lei dos Senos e dos Cossenos
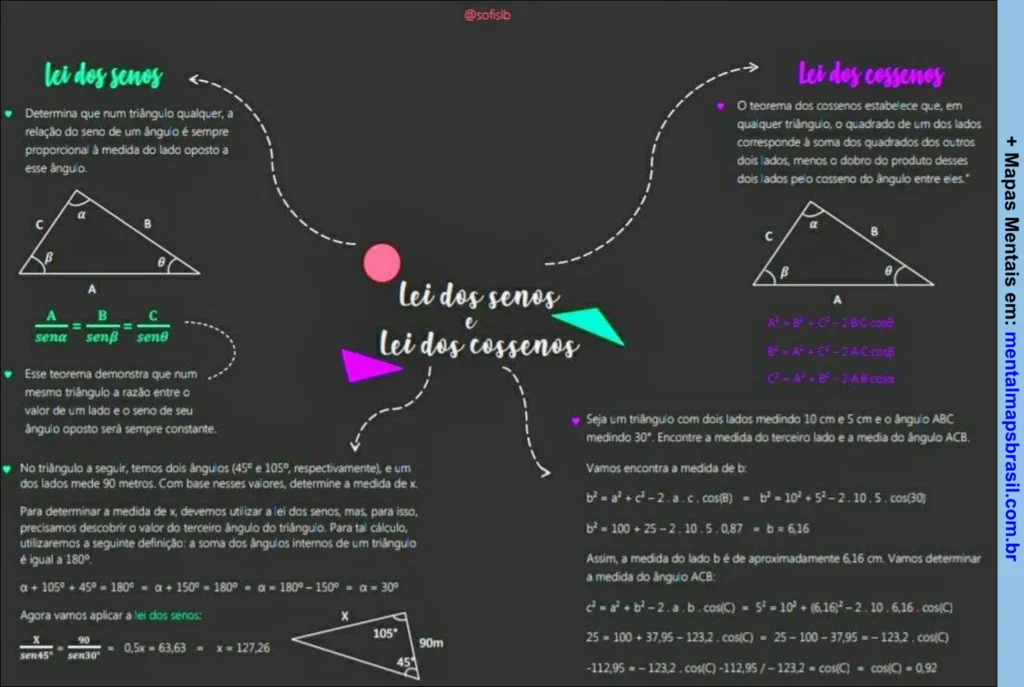
Lei dos Senos: Determina que num triângulo qualquer, a relação do seno de um ângulo é sempre proporcional à medida do lado oposto a esse ângulo.
Esse teorema demonstra que num mesmo triângulo a razão entre o valor de um lado e o seno de seu ângulo oposto será sempre constante.
No triângulo a seguir, temos dois ângulos (45° e 105°, respectivamente), e um dos lados mede 90 metros. Com base nesses valores, determina a medida de x.
Para determinar a medida de x, devemos utilizar a lei dos senos, mas, para isso, precisamos descobrir o valor do terceiro ângulo do triângulo. Para tal cálculo, utilizaremos a seguinte definição: a soma dos ângulos internos de um triângulo é igual a 180°.
Continue lendo…
O teorema dos cossenos estabelece que, em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles. a² = b² + c² – 2bc.cosα, b² = a² + c² – 2ac.cosβ, c² = a² + b² – 2ab.cosθ. Seja um triângulo com dois lados medindo 10 cm e 5 cm e o ângulo ABC medindo 30º. Encontre a medida do terceiro lado e a media do ângulo ACB.
Mapa Mental sobre Lei dos Senos e Cossenos: Fórmulas e Aplicações
Transcrição do Mapa Mental sobre Lei dos Senos
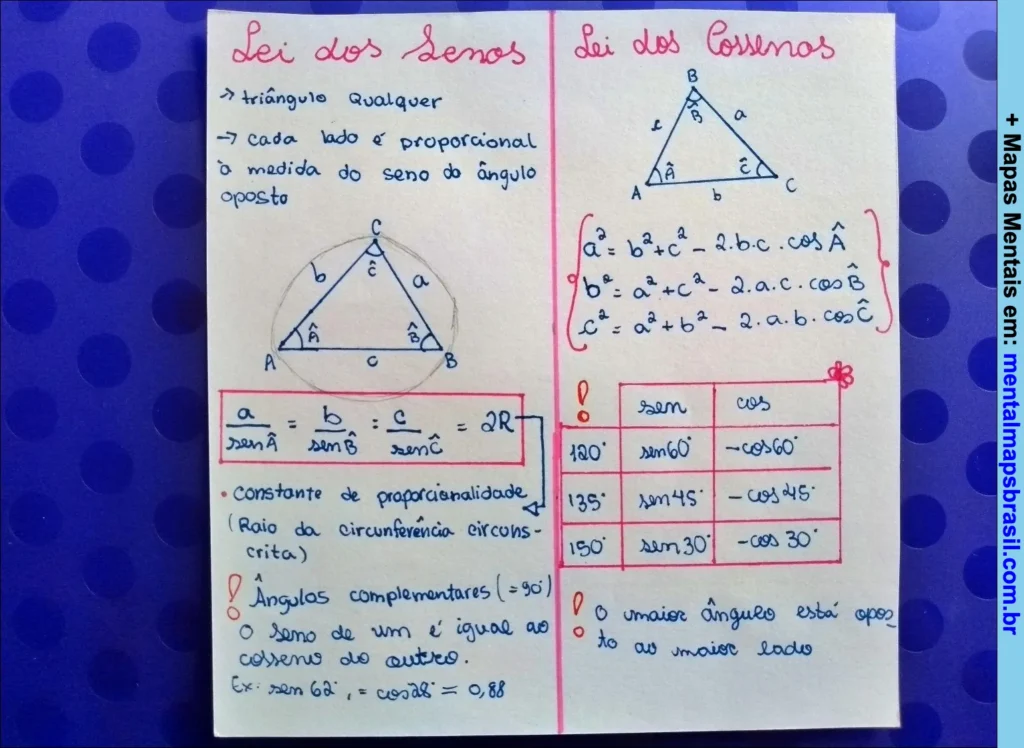
triângulo qualquer
cada lado é proporcional à medida do seno do ângulo oposto
a/sen  = b/sen B̂ = c/sen Ĉ = 2R
constante de proporcionalidade (Raio da circunferência circunscrita)
Ângulos complementares (= 90°)
O seno de um é igual ao cosseno do outro.
Ex: sen 68° = cos22° = 0,88
Continue lendo…
Lei dos Cossenos
a² = b² + c² – 2.b.c.cos Â
b² = a² + c² – 2.a.c.cos B̂
c² = a² + b² – 2.a.b.cos Ĉ
sen cos
120° | sen60° | -cos60°
135° | sen45° | -cos45°
150° | sen30° | -cos30°
O maior ângulo está oposto ao maior lado